Calculus Integration Cheat Sheet - For each factor in the denominator we get term(s) in the decomposition according to the. Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. Familiarize yourself with basic geometric formulas (e.g., areas of rectangles, triangles, circles) for simple integral evaluations. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx. Symbolab integrals cheat sheet common integrals: ∫𝑥−1 𝑥=ln(𝑥) ∫ 𝑥 𝑥 =ln(𝑥) ∫ |𝑥 𝑥=𝑥√𝑥 2 2 ∫ 𝑥 𝑥= 𝑥 ∫sin(𝑥) 𝑥=−cos(𝑥) ∫cos(𝑥) 𝑥=sin(𝑥) trigonometric. Mastering integration is a crucial aspect of calculus, and having a comprehensive understanding of the various rules and. Integrate the partial fraction decomposition (p.f.d.).
Symbolab integrals cheat sheet common integrals: Mastering integration is a crucial aspect of calculus, and having a comprehensive understanding of the various rules and. For each factor in the denominator we get term(s) in the decomposition according to the. Integrate the partial fraction decomposition (p.f.d.). ∫𝑥−1 𝑥=ln(𝑥) ∫ 𝑥 𝑥 =ln(𝑥) ∫ |𝑥 𝑥=𝑥√𝑥 2 2 ∫ 𝑥 𝑥= 𝑥 ∫sin(𝑥) 𝑥=−cos(𝑥) ∫cos(𝑥) 𝑥=sin(𝑥) trigonometric. Familiarize yourself with basic geometric formulas (e.g., areas of rectangles, triangles, circles) for simple integral evaluations. Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx.
Symbolab integrals cheat sheet common integrals: Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. ∫𝑥−1 𝑥=ln(𝑥) ∫ 𝑥 𝑥 =ln(𝑥) ∫ |𝑥 𝑥=𝑥√𝑥 2 2 ∫ 𝑥 𝑥= 𝑥 ∫sin(𝑥) 𝑥=−cos(𝑥) ∫cos(𝑥) 𝑥=sin(𝑥) trigonometric. Mastering integration is a crucial aspect of calculus, and having a comprehensive understanding of the various rules and. For each factor in the denominator we get term(s) in the decomposition according to the. Integrate the partial fraction decomposition (p.f.d.). Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx. Familiarize yourself with basic geometric formulas (e.g., areas of rectangles, triangles, circles) for simple integral evaluations.
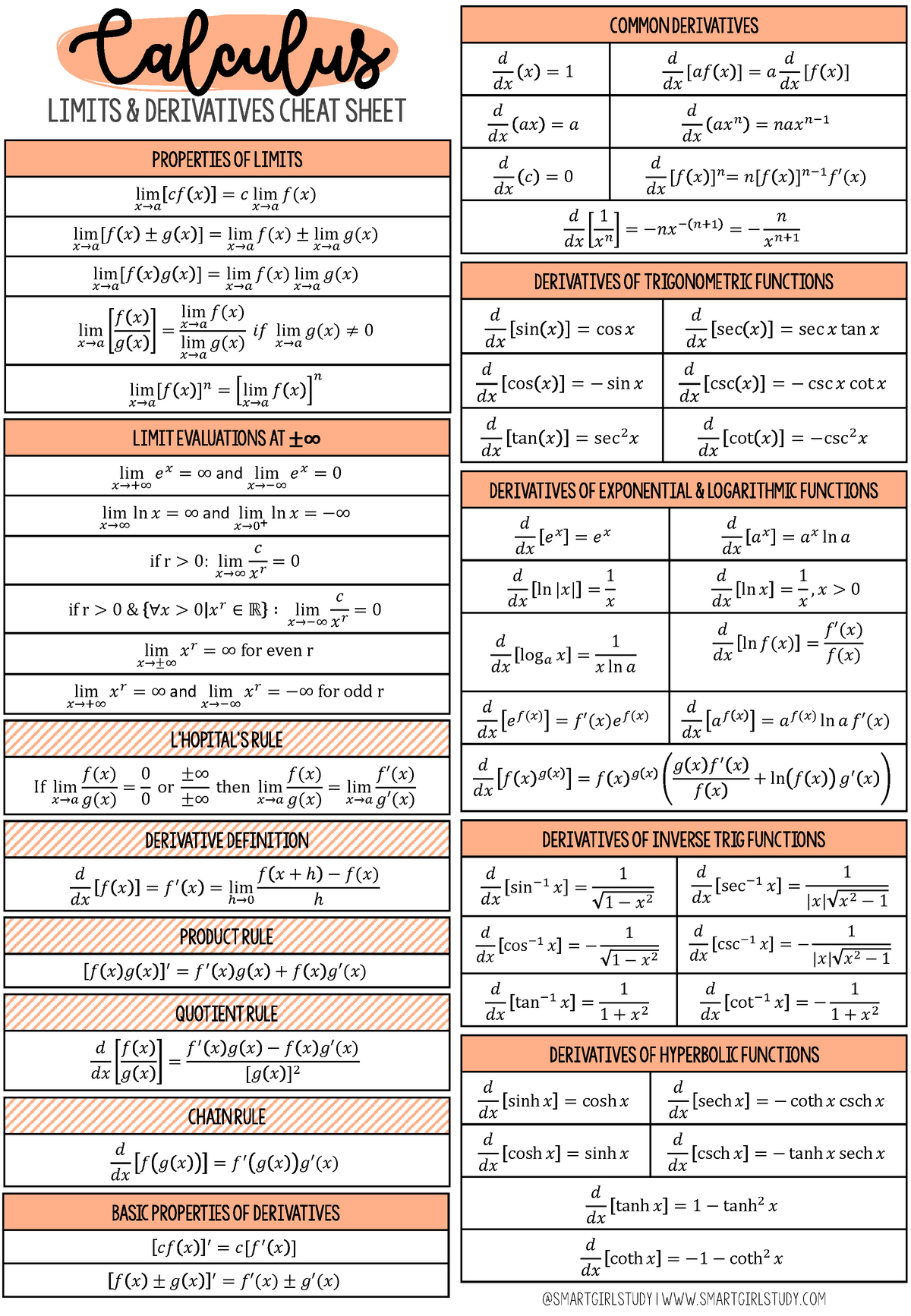
Integral Cheat Sheet Calculus derivative calc trig hyperbolic integral
Symbolab integrals cheat sheet common integrals: Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx. Familiarize yourself with basic geometric formulas (e.g., areas of rectangles, triangles, circles) for simple integral evaluations. ∫𝑥−1 𝑥=ln(𝑥) ∫ 𝑥 𝑥 =ln(𝑥) ∫ |𝑥 𝑥=𝑥√𝑥 2 2 ∫ 𝑥 𝑥= 𝑥 ∫sin(𝑥) 𝑥=−cos(𝑥) ∫cos(𝑥) 𝑥=sin(𝑥) trigonometric. Integrate the.
Final Practice Exam MATH 2780 Volume Optimization & Flux Calculations
∫𝑥−1 𝑥=ln(𝑥) ∫ 𝑥 𝑥 =ln(𝑥) ∫ |𝑥 𝑥=𝑥√𝑥 2 2 ∫ 𝑥 𝑥= 𝑥 ∫sin(𝑥) 𝑥=−cos(𝑥) ∫cos(𝑥) 𝑥=sin(𝑥) trigonometric. For each factor in the denominator we get term(s) in the decomposition according to the. Symbolab integrals cheat sheet common integrals: Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx. Familiarize yourself with.
SOLUTION Calculus Cheat Sheet Integrals Studypool
Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. Mastering integration is a crucial aspect of calculus, and having a comprehensive understanding of the various rules and. Integrate the partial fraction decomposition (p.f.d.). For each factor in the denominator we get term(s) in the decomposition.
Bc Calculus Cheat Sheet Download Printable PDF Templateroller
Integrate the partial fraction decomposition (p.f.d.). Symbolab integrals cheat sheet common integrals: ∫𝑥−1 𝑥=ln(𝑥) ∫ 𝑥 𝑥 =ln(𝑥) ∫ |𝑥 𝑥=𝑥√𝑥 2 2 ∫ 𝑥 𝑥= 𝑥 ∫sin(𝑥) 𝑥=−cos(𝑥) ∫cos(𝑥) 𝑥=sin(𝑥) trigonometric. Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. Mastering integration is a.
Calculus Derivatives And Limits Sheet To Download And vrogue.co
For each factor in the denominator we get term(s) in the decomposition according to the. Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. Symbolab integrals cheat sheet common integrals: Familiarize yourself with basic geometric formulas (e.g., areas of rectangles, triangles, circles) for simple integral.
Integral cheat sheet Docsity
∫𝑥−1 𝑥=ln(𝑥) ∫ 𝑥 𝑥 =ln(𝑥) ∫ |𝑥 𝑥=𝑥√𝑥 2 2 ∫ 𝑥 𝑥= 𝑥 ∫sin(𝑥) 𝑥=−cos(𝑥) ∫cos(𝑥) 𝑥=sin(𝑥) trigonometric. Integrate the partial fraction decomposition (p.f.d.). Mastering integration is a crucial aspect of calculus, and having a comprehensive understanding of the various rules and. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx..
Calculus Integrals Reference Sheet (with Formulas) EEWeb
Symbolab integrals cheat sheet common integrals: ∫𝑥−1 𝑥=ln(𝑥) ∫ 𝑥 𝑥 =ln(𝑥) ∫ |𝑥 𝑥=𝑥√𝑥 2 2 ∫ 𝑥 𝑥= 𝑥 ∫sin(𝑥) 𝑥=−cos(𝑥) ∫cos(𝑥) 𝑥=sin(𝑥) trigonometric. Mastering integration is a crucial aspect of calculus, and having a comprehensive understanding of the various rules and. Integrate the partial fraction decomposition (p.f.d.). Integral is called convergent if the limit exists and has.
Calculus 2 Cheat Sheet
Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx. Familiarize yourself with basic geometric formulas (e.g., areas of rectangles, triangles, circles) for simple integral evaluations. Symbolab integrals cheat sheet.
Integration Rules Cheat Sheet
Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx. For each factor in the denominator we get term(s) in the decomposition according to the. Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. Symbolab integrals cheat sheet common.
Calc 1 Columbia Engineering Hub
Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx. Familiarize yourself with basic geometric formulas (e.g., areas of rectangles, triangles, circles) for simple integral evaluations. Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. Integrate the partial fraction.
Symbolab Integrals Cheat Sheet Common Integrals:
Mastering integration is a crucial aspect of calculus, and having a comprehensive understanding of the various rules and. Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx. Familiarize yourself with basic geometric formulas (e.g., areas of rectangles, triangles, circles) for simple integral evaluations.
Integrate The Partial Fraction Decomposition (P.f.d.).
For each factor in the denominator we get term(s) in the decomposition according to the. ∫𝑥−1 𝑥=ln(𝑥) ∫ 𝑥 𝑥 =ln(𝑥) ∫ |𝑥 𝑥=𝑥√𝑥 2 2 ∫ 𝑥 𝑥= 𝑥 ∫sin(𝑥) 𝑥=−cos(𝑥) ∫cos(𝑥) 𝑥=sin(𝑥) trigonometric.